丂傛偔偁傞偛幙栤(FAQ)
峾娗幃杊攇掔4
俻.丂寁嶼撪梕
- 摴楬嫶帵曽彂偵傛傞抧斦斀椡僶僱學悢偼偳偺傛偆偵嶼掕偝傟偰偄傑偡偐
- 峾娗幃杊攇掔偺昗弨揑側愝寁庤弴偱丄杮僔僗僥儉偑懳墳偟偰偄傞売強傪嫵偊偰壓偝偄
- 曄埵朄偲僼儗乕儉夝愅偱寁嶼寢壥偵杦偳嵎偑側偄偺偼偳偆偟偰偱偡偐
- 壛懍搙墳摎僗儁僋僩儖傛傝愝寁恔搙傪嶼掕偡傞嵺偵偼偳偺傛偆側偙偲偵拲堄偡傟偽椙偄偱偡偐
- 峐偲僼乕僠儞僌偺寢崌寁嶼偱巊梡偟偰偄傞塱媣壸廳偺倁丒俫丒俵偲曄摦壸廳偺倁丒俫丒俵偼偳偺條偵偟偰寁嶼偟偨抣側偺偱偟傚偆偐
- 愝寁恔搙偵偍偗傞屌桳廃婜偺嶼掕偵梡偄傞僶僱掕悢偼偳偺傛偆偵偟偰寁嶼偟偰偄傞偺偱偟傚偆偐
- 挔昜偵昞帵偟偰偁傞摍壙愡揰椡偼偳偺傛偆偵埖傢傟偰偄傞偺偐
- 僼乕僠儞僌偺峐抂晹偺墴偟敳偒偣傫抐墳椡搙偺寁嶼忦審偵偮偄偰嫵偊偰壓偝偄
- 抧斦斀椡學悢傪媮傔傞嵺偵丄寁嶼曽朄偲偟偰棙梡偡傞乭N抣仺Kh乭傪慖戰偟偨帪偺qu=N/X(N/mm2乯偲偄偆幃偼偳偺傛偆側暥專傪巊梡偝傟偨偺偱偟傚偆偐
- 僇乕僥儞幃杊攇掔丄帺棫峾娗幃杊攇掔偵攇埑摍偑嶌梡偡傞嵺偺寁嶼嵹壸暆偼偳偺傛偆偵峫偊偰偄傑偡偐
- 揝斅旐暍傪専摙偟偨応崌丄偳偺傛偆側抐柺彅尦偱寁嶼偝傟傑偡偐
- 摍壙愡揰椡傪嶌梡偝偣偰抐柺椡偺寁嶼傪峴偆応崌偵僇乕僥儞斉偺帺廳傪峫椂偡傞偺偼壸廳偺廳暋偵側傝偍偐偟偄偺偱偼側偄偱偟傚偆偐
- 嫋梕墳椡搙朄偺応崌丄攇埑帪偺寁嶼偱攇偺嶳偑嶌梡偡傞応崌偲攇偺扟偑嶌梡偡傞応崌偱丄嫋梕抣偑堎側傞偺偼壗屘偱偡偐丠乮攇偺嶳丗忢帪丄攇偺扟丟堎忢帪乯
俻.丂嶲峫暥專
俻.丂愝掕
俻仌俙.丂寁嶼撪梕
- 摴楬嫶帵曽彂偵傛傞抧斦斀椡僶僱學悢偼偳偺傛偆偵嶼掕偝傟偰偄傑偡偐
- 峾娗幃杊攇掔偺昗弨揑側愝寁庤弴偱丄杮僔僗僥儉偑懳墳偟偰偄傞売強傪嫵偊偰壓偝偄
- 曄埵朄偲僼儗乕儉夝愅偱寁嶼寢壥偵杦偳嵎偑側偄偺偼偳偆偟偰偱偡偐
- 壛懍搙墳摎僗儁僋僩儖傛傝愝寁恔搙傪嶼掕偡傞嵺偵偼偳偺傛偆側偙偲偵拲堄偡傟偽椙偄偱偡偐
- 峐偲僼乕僠儞僌偺寢崌寁嶼偱巊梡偟偰偄傞塱媣壸廳偺倁丒俫丒俵偲曄摦壸廳偺倁丒俫丒俵偼偳偺條偵偟偰寁嶼偟偨抣側偺偱偟傚偆偐
- 愝寁恔搙偵偍偗傞屌桳廃婜偺嶼掕偵梡偄傞僶僱掕悢偼偳偺傛偆偵偟偰寁嶼偟偰偄傞偺偱偟傚偆偐
- 挔昜偵昞帵偟偰偁傞摍壙愡揰椡偼偳偺傛偆偵埖傢傟偰偄傞偺偐
- 僼乕僠儞僌偺峐抂晹偺墴偟敳偒偣傫抐墳椡搙偺寁嶼忦審偵偮偄偰嫵偊偰壓偝偄
- 抧斦斀椡學悢傪媮傔傞嵺偵丄寁嶼曽朄偲偟偰棙梡偡傞乭N抣仺Kh乭傪慖戰偟偨帪偺qu=N/X(N/mm2乯偲偄偆幃偼偳偺傛偆側暥專傪巊梡偝傟偨偺偱偟傚偆偐
- 僇乕僥儞幃杊攇掔丄帺棫峾娗幃杊攇掔偵攇埑摍偑嶌梡偡傞嵺偺寁嶼嵹壸暆偼偳偺傛偆偵峫偊偰偄傑偡偐
- 揝斅旐暍傪専摙偟偨応崌丄偳偺傛偆側抐柺彅尦偱寁嶼偝傟傑偡偐
- 摍壙愡揰椡傪嶌梡偝偣偰抐柺椡偺寁嶼傪峴偆応崌偵僇乕僥儞斉偺帺廳傪峫椂偡傞偺偼壸廳偺廳暋偵側傝偍偐偟偄偺偱偼側偄偱偟傚偆偐
- 嫋梕墳椡搙朄偺応崌丄攇埑帪偺寁嶼偱攇偺嶳偑嶌梡偡傞応崌偲攇偺扟偑嶌梡偡傞応崌偱丄嫋梕抣偑堎側傞偺偼壗屘偱偡偐丠乮攇偺嶳丗忢帪丄攇偺扟丟堎忢帪乯
専摙懳徾偺搚憌偑偁傞峐偵懳偟偰丄侾乛β嬫娫偱偺β偺寁嶼傪峴偄
偦偺抣傪婎偵寁嶼嵹壸暆BH傪嶼掕丄偙偺抣傪婎偵寁嶼傪峴偄傑偡丅
峾娗峐偺宎傪俢偲偟偨応崌丄β偼師幃偱嶼掕偝傟傑偡丅

侾乛β嬫娫偑懡憌抧斦偺応崌丄
峾娗峐偱巊梡偡傞β偼廂懇寁嶼偵傛偭偰嶼掕傪峴偄傑偡丅
偦偺抣傪婎偵寁嶼嵹壸暆BH傪嶼掕丄偙偺抣傪婎偵寁嶼傪峴偄傑偡丅
峾娗峐偺宎傪俢偲偟偨応崌丄β偼師幃偱嶼掕偝傟傑偡丅

侾乛β嬫娫偑懡憌抧斦偺応崌丄
峾娗峐偱巊梡偡傞β偼廂懇寁嶼偵傛偭偰嶼掕傪峴偄傑偡丅
00383
杮僔僗僥儉偱偼
丒抧恔攇宍傪梡偄傞嵺偵昁梫側壖憐抧昞柺偐傜侾乛β偺埵抲
丒屌桳廃婜
丒懳徾抧恔偺壛懍搙墳摎僗儁僋僩儖
丒愝寁恔搙
丒抐柺惈擻徠嵏乮峐斀椡乛峐墳椡丄崻擖傟挿丄巟帩椡丄晧偺廃柺杸嶤丄峐摢晹乯
埲忋偺崁栚偑峴偊傑偡丅
丒侾乛β埵抲偱偺懳徾抧恔偺壛懍搙攇宍偺嶼掕
偙偪傜偼暰幮惢昳乽徠嵏梡恔搙嶼弌乿傑偨偼抧恔帪偺塼忬壔偵傛傞峔憿暔旐奞梊應僾儘僌儔儉乽FLIP乿傪巊梡偟傑偡丅
丒嵶晹愝寁乮忋晹岺偺愝寁乯
偙偪傜偼峾娗幃杊攇掔偺峔憿宍幃偵墳偠偰暰幮惢昳乽峾娗幃丒栴斅幃忋晹岺乿傪巊梡偟傑偡丅
00801
曄埵朄偱巊梡偝傟偰偄傞揱払儅僩儕僋僗丄僼儗乕儉夝愅偱巊梡偝傟偰偄傞崉惈儅僩儕僋僗偑嫟偵摨偠旝暘曽掱幃偑婎偵側偭偰峔惉偝傟偰偄傞偨傔偱偡丅曄埵朄偲僼儗乕儉夝愅偱偼壸廳偺嶌梡曽朄偵庒姳堘偄偼偁傝傑偡偑丄偦傟埲奜偼傎傏摨偠偱偡偺偱丄偦偺偨傔寢壥偵戝偒側堘偄偼偁傝傑偣傫丅
00399
杮僔僗僥儉偱偼堦師尦抧恔墳摎夝愅偵傛偭偰媮傔傜傟偨壖憐抧昞柺偐傜侾乛β偺埵抲偺抧恔攇宍傪梡偄偰壛懍搙墳摎僗儁僋僩儖傪嶼弌偟丄傑偨丄峾娗幃杊攇掔偺僼儗乕儉夝愅傪峴偄丄悈暯曄埵偲嶌梡偡傞悈暯椡偐傜峾娗幃杊攇掔偺僶僱掕悢傪嶼弌偟丄屌桳廃婜傪媮傔傑偡丅
偙偺壛懍搙墳摎僗儁僋僩儖偲墶嶸嫶偺屌桳廃婜偐傜愝寁恔搙偑媮傑傝傑偡丅
偙偺帪丄拲堄偡傋偒揰偲偟偰
丒抧恔攇宍傪梡偄傞嵺偵昁梫側壖憐抧昞柺偐傜侾乛β偺埵抲
丒屌桳廃婜
偙偺俀崁栚偺抣偑曄峏偝傟傞応崌偵偼嵞搙愝寁恔搙傪寁嶼偡傞昁梫偑偁傝傑偡丅
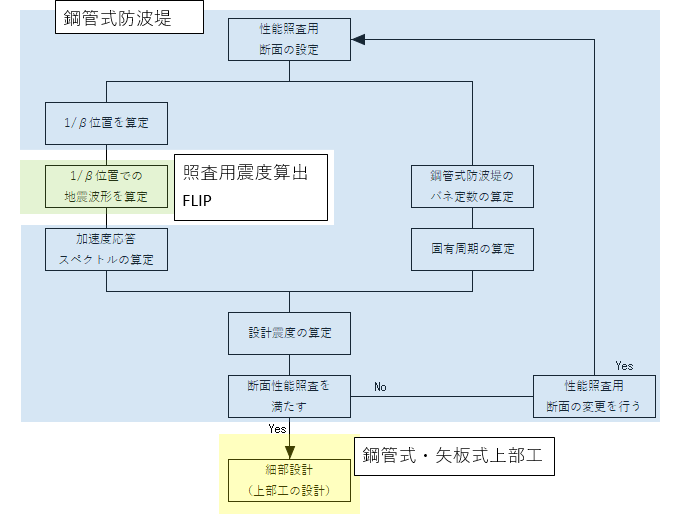
偙傟傜偺寁嶼偺棳傟傪偲傝傑偲傔偨偺偑埲壓偺寁嶼庤弴僼儘乕偵側傝傑偡丅
壖憐抧昞柺偺侾乛β偺抣偑曄峏偝傟傞崁栚偲偟偰偼峐宎丄峐偺擏岤丄搚幙忦審偑峫偊傜傟傑偡丅
偙偺応崌偵偼嵞搙堦師尦抧恔墳摎夝愅偵傛傝抧恔攇宍傪嶼弌偟側偗傟偽側傝傑偣傫丅
峾娗幃杊攇掔偺屌桳廃婜偺抣偑曄峏偝傟傞崁栚偲偟偰偼忋晹岺偺宍忬丄峐杮悢丄峐愝抲娫妘丄峐悺朄丄搚幙忦審摍懡婒偵搉傝傑偡丅
愝寁恔搙偺寁嶼庤弴丒徻嵶偵偮偄偰偼
峘榩偺巤愝偲媄弍忋偺婎弨丒摨夝愢乮拞姫乯丂P1208乣1209偵宖嵹偝傟偰偍傝傑偡丅
偙偺壛懍搙墳摎僗儁僋僩儖偲墶嶸嫶偺屌桳廃婜偐傜愝寁恔搙偑媮傑傝傑偡丅
偙偺帪丄拲堄偡傋偒揰偲偟偰
丒抧恔攇宍傪梡偄傞嵺偵昁梫側壖憐抧昞柺偐傜侾乛β偺埵抲
丒屌桳廃婜
偙偺俀崁栚偺抣偑曄峏偝傟傞応崌偵偼嵞搙愝寁恔搙傪寁嶼偡傞昁梫偑偁傝傑偡丅
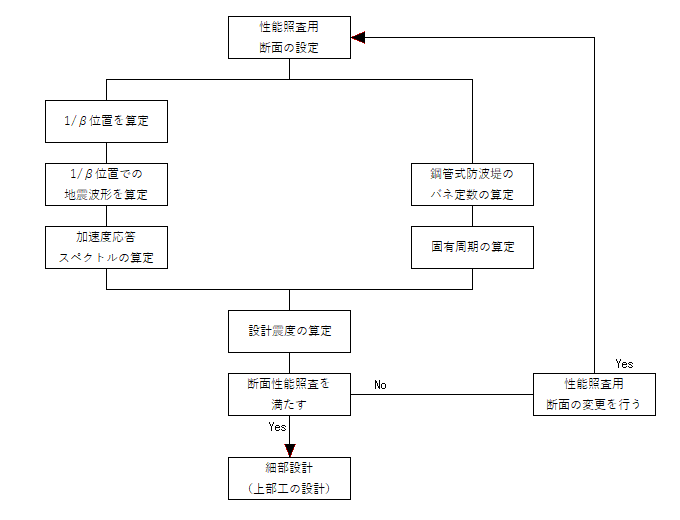
偙傟傜偺寁嶼偺棳傟傪偲傝傑偲傔偨偺偑埲壓偺寁嶼庤弴僼儘乕偵側傝傑偡丅

壖憐抧昞柺偺侾乛β偺抣偑曄峏偝傟傞崁栚偲偟偰偼峐宎丄峐偺擏岤丄搚幙忦審偑峫偊傜傟傑偡丅
偙偺応崌偵偼嵞搙堦師尦抧恔墳摎夝愅偵傛傝抧恔攇宍傪嶼弌偟側偗傟偽側傝傑偣傫丅
峾娗幃杊攇掔偺屌桳廃婜偺抣偑曄峏偝傟傞崁栚偲偟偰偼忋晹岺偺宍忬丄峐杮悢丄峐愝抲娫妘丄峐悺朄丄搚幙忦審摍懡婒偵搉傝傑偡丅
愝寁恔搙偺寁嶼庤弴丒徻嵶偵偮偄偰偼
峘榩偺巤愝偲媄弍忋偺婎弨丒摨夝愢乮拞姫乯丂P1208乣1209偵宖嵹偝傟偰偍傝傑偡丅
00800
塱媣壸廳偺倁丒俫丒俵偼忋晹岺帺廳丒晜椡偺傒偱峐摢嶌梡椡傪寁嶼偟偨傕偺偱曄摦壸廳偺倁丒俫丒俵偼攇椡偺傒偱寁嶼偟偨抣偱偡丅
00560
崪慻峔憿夝愅偵偰峔憿暔偵悈暯椡傪嶌梡偝偣丄嶼弌偟偨峔憿暔偺悈暯曄埵傪嶌梡偝偣偨悈暯椡偱妱傞帠偱嶼掕偝傟傑偡丅
崪慻峔憿夝愅偼慄宍抏惈傪慜採偲偟偨寁嶼偱偡偺偱丄悈暯椡偲悈暯曄埵偼斾椺偺娭學偵側傝傑偡丅
傛偭偰丄嶌梡偝偣傞悈暯椡偼偳傫側抣偱偁偭偰傕丄峔憿暔偺僶僱掕悢偼堦掕偵側傝傑偡丅
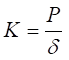
偙偙偵
K:峔憿暔偺僶僱掕悢
P:悈暯椡
δ:悈暯曄埵
崪慻峔憿夝愅偼慄宍抏惈傪慜採偲偟偨寁嶼偱偡偺偱丄悈暯椡偲悈暯曄埵偼斾椺偺娭學偵側傝傑偡丅
傛偭偰丄嶌梡偝偣傞悈暯椡偼偳傫側抣偱偁偭偰傕丄峔憿暔偺僶僱掕悢偼堦掕偵側傝傑偡丅
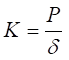
偙偙偵
K:峔憿暔偺僶僱掕悢
P:悈暯椡
δ:悈暯曄埵
00021
尨揰偺曄埵傪寁嶼偡傞偺偵巊梡偟偰偍傝傑偡丅
偙偙偵偁傞摍壙愡揰椡偼奺峐偵嶌梡偡傞抐柺椡傪寁嶼偡傞摍壙愡揰椡偲摨偠傕偺偱偼偁傝傑偣傫丅
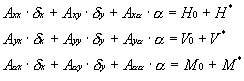
偙偙偵偁傞摍壙愡揰椡偼奺峐偵嶌梡偡傞抐柺椡傪寁嶼偡傞摍壙愡揰椡偲摨偠傕偺偱偼偁傝傑偣傫丅
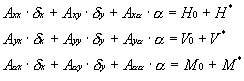
00371
慜峐偺応崌偼慜峐偵嶌梡偡傞悈暯椡偑惓偺偲偒
屻峐偺応崌偼屻峐偵嶌梡偡傞悈暯椡偑晧偺偲偒
偦傟偧傟専摙傪峴偄傑偡丅
屻峐偺応崌偼屻峐偵嶌梡偡傞悈暯椡偑晧偺偲偒
偦傟偧傟専摙傪峴偄傑偡丅
00377
堦斒幮抍朄恖丂峾娗峐丒峾栴斅媄弍嫤夛乽峾栴斅丂愝寁偐傜巤岺傑偱乿2014擭夵掶怴斉
P102偵婰嵹偝傟偰偄傑偡丅
P102偵婰嵹偝傟偰偄傑偡丅
00625
杮僔僗僥儉偱偼
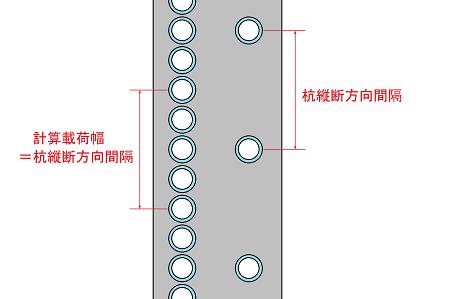
僇乕僥儞幃杊攇掔偺応崌
峐廲抐娫妘傪寁嶼嵹壸暆偲偟偰愝掕偟偰偄傑偡丅
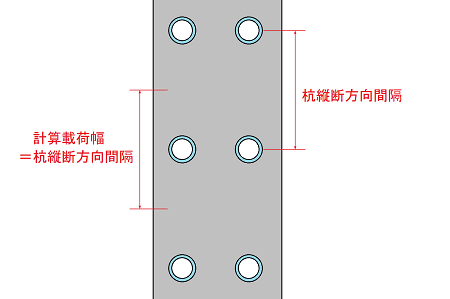
帺棫峾娗幃杊攇掔偱峾嵽杮悢偑侾杮偺応崌
栴斅偺奜宎亄宲庤桳岠娫妘傪寁嶼嵹壸暆偲偟偰愝掕偟偰偄傑偡丅
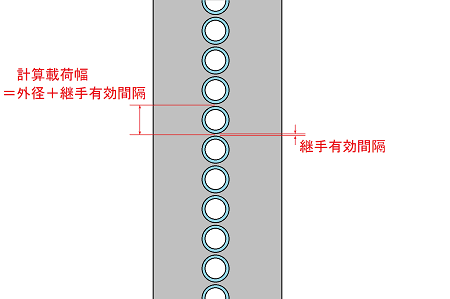
帺棫峾娗幃杊攇掔偱峾嵽杮悢偑俀杮埲忋偺応崌
峐廲抐曽岦娫妘傪寁嶼嵹壸暆偲偟偰愝掕偟偰偄傑偡丅
僇乕僥儞幃杊攇掔偺応崌
峐廲抐娫妘傪寁嶼嵹壸暆偲偟偰愝掕偟偰偄傑偡丅

帺棫峾娗幃杊攇掔偱峾嵽杮悢偑侾杮偺応崌
栴斅偺奜宎亄宲庤桳岠娫妘傪寁嶼嵹壸暆偲偟偰愝掕偟偰偄傑偡丅

帺棫峾娗幃杊攇掔偱峾嵽杮悢偑俀杮埲忋偺応崌
峐廲抐曽岦娫妘傪寁嶼嵹壸暆偲偟偰愝掕偟偰偄傑偡丅

00403
揝斅旐暍偺専摙偼巆懚懴椡傪峫椂偣偢偵寁嶼偟傑偡丅偮傑傝丄旐暍慜偺峾娗峐傪柍帇偟偰揝斅偺傒偺抐柺彅尦偱徠嵏偟傑偡丅
01128
摍壙愡揰壸廳偼峐扨懱偵嶌梡偡傞壸廳偵懳偟偰偺曄埵検偵懳偟偰偐偐偭偰偄傞偲尒傜傟傞壸廳偱偡丅
椺偊偽恾亅1偺傛偆側峐偑偁偭偨偲偟傑偡丅
偙偺応崌丄峐偼壓偺恾亅2偺傛偆偵曄埵偟傑偡丅
幚嵺丄偙偺傛偆偵曄埵偟偰偄傞偺偱偡偑峐摢晹偵偼壗偺椡傕壛傢偭偰偼偄傑偣傫丅
偦偙偱恾亅3偺傛偆偵丄偙偺峐偑尦偺埵抲偐傜崱偺埵抲傑偱曄埵偟偨偲偒偵峐摢晹偵偐偐偭偰偄傞偲壖掕偟偨椡丄偙傟偑摍壙愡揰椡偵側傝傑偡丅
偙傟偼偁偔傑偱峐摢晹偵嶌梡偟偰偄傞偲壖掕偟偰偄傞椡偱偁偭偰幚嵺偵偐偐偭偰偄傞椡偱偼偁傝傑偣傫丅
偦偺屻丄偙偺摍壙愡揰壸廳傪梡偄偰奺晹嵽偺曄埵偑媮傑傝傑偡丅
偙偺曄埵傪婎偵晹嵽偺抐柺椡傪媮傔偰偄偔偺偱偡偑丄曄埵傪媮傔偰偄偔偺偵恾亅1仺恾亅3偺傛偆偵幚嵺偺忬懺偐傜尒偐偗偺忬懺偵壖掕偟偰寁嶼傪恑傔偰偒傑偟偨丅
偦偺偨傔晹嵽偺抐柺椡傪媮傔傞偵偼恾亅3仺恾亅1偲偄偆晽偵尒偐偗偺忬懺偐傜幚嵺偺忬懺偵栠偟偰寁嶼傪偍偙側傢側偗傟偽側傝傑偣傫丅
峐摢晹偵偐偐傞抐柺椡俥偼峐摢晹偺曄埵検傪δ偲偟峐摢晹偺偽偹掕悢傪俲偲偡傞偲僼僢僋偺朄懃偵傛傝
F=俲δ丂丂偲側傝傑偡丅
偟偐偟丄尒偐偗偺壸廳偱偁傞摍壙愡揰壸廳w傪峐摢晹偵峫椂偟偰偄傞偺偱偙傟傪徚嫀偡傞昁梫偑偁傝傑偡丅
傛偭偰
F=Kδ亅w
偙傟偑峐摢晹偵嶌梡偡傞惓偟偄抐柺椡偵側傝傑偡丅
偱偼峐偺擟堄偺揰偱偺抐柺椡傪媮傔傞応崌丄恾亅4偺傛偆偵
峐摢晹偐傜x(m)棧傟偨揰P偱偺幉椡Fp傪媮傔傞応崌丄峐摢晹偺幉椡傪F丄峐偵嶌梡偡傞墧捈曽岦偺摍暘晍壸廳傪倲偲偡傞偲
Fp亖F + t丒x
偵側傝傑偡丅
椺偊偽恾亅1偺傛偆側峐偑偁偭偨偲偟傑偡丅
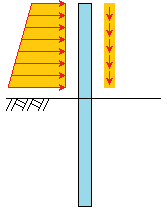 |
| 恾亅1 |
偙偺応崌丄峐偼壓偺恾亅2偺傛偆偵曄埵偟傑偡丅
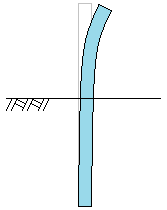 |
| 恾亅2 |
幚嵺丄偙偺傛偆偵曄埵偟偰偄傞偺偱偡偑峐摢晹偵偼壗偺椡傕壛傢偭偰偼偄傑偣傫丅
偦偙偱恾亅3偺傛偆偵丄偙偺峐偑尦偺埵抲偐傜崱偺埵抲傑偱曄埵偟偨偲偒偵峐摢晹偵偐偐偭偰偄傞偲壖掕偟偨椡丄偙傟偑摍壙愡揰椡偵側傝傑偡丅
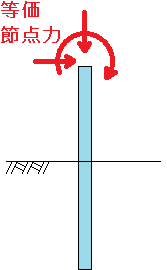 |
| 恾亅3 |
偙傟偼偁偔傑偱峐摢晹偵嶌梡偟偰偄傞偲壖掕偟偰偄傞椡偱偁偭偰幚嵺偵偐偐偭偰偄傞椡偱偼偁傝傑偣傫丅
偦偺屻丄偙偺摍壙愡揰壸廳傪梡偄偰奺晹嵽偺曄埵偑媮傑傝傑偡丅
偙偺曄埵傪婎偵晹嵽偺抐柺椡傪媮傔偰偄偔偺偱偡偑丄曄埵傪媮傔偰偄偔偺偵恾亅1仺恾亅3偺傛偆偵幚嵺偺忬懺偐傜尒偐偗偺忬懺偵壖掕偟偰寁嶼傪恑傔偰偒傑偟偨丅
偦偺偨傔晹嵽偺抐柺椡傪媮傔傞偵偼恾亅3仺恾亅1偲偄偆晽偵尒偐偗偺忬懺偐傜幚嵺偺忬懺偵栠偟偰寁嶼傪偍偙側傢側偗傟偽側傝傑偣傫丅
峐摢晹偵偐偐傞抐柺椡俥偼峐摢晹偺曄埵検傪δ偲偟峐摢晹偺偽偹掕悢傪俲偲偡傞偲僼僢僋偺朄懃偵傛傝
F=俲δ丂丂偲側傝傑偡丅
偟偐偟丄尒偐偗偺壸廳偱偁傞摍壙愡揰壸廳w傪峐摢晹偵峫椂偟偰偄傞偺偱偙傟傪徚嫀偡傞昁梫偑偁傝傑偡丅
傛偭偰
F=Kδ亅w
偙傟偑峐摢晹偵嶌梡偡傞惓偟偄抐柺椡偵側傝傑偡丅
偱偼峐偺擟堄偺揰偱偺抐柺椡傪媮傔傞応崌丄恾亅4偺傛偆偵
 |
| 恾亅4 |
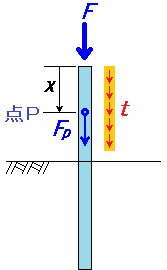
峐摢晹偐傜x(m)棧傟偨揰P偱偺幉椡Fp傪媮傔傞応崌丄峐摢晹偺幉椡傪F丄峐偵嶌梡偡傞墧捈曽岦偺摍暘晍壸廳傪倲偲偡傞偲
Fp亖F + t丒x
偵側傝傑偡丅
00562
峾娗幃杊攇掔偼攇偺扟嶌梡帪偵梘埑椡偺愝掕偑偱偒傑偡丅
乽梘埑椡傪峫椂偟偨応崌偼丄堎忢帪偲偟偰偺埨慡棪丄嫋梕墳椡搙偵傛傝愝寁偡傞偺偑傛偄乿偲乽嫏峘丒嫏応偺巤愝偺愝寁嶲峫恾彂 2015擭斉 [忋]乿偺p412偵婰嵹偑偁傝傑偡丅
偦偺偨傔丄梘埑椡傪峫椂偟偨応崌偼攇偺扟偲攇偺嶳偱嫋梕抣偑堎側傝傑偡丅
乽梘埑椡傪峫椂偟偨応崌偼丄堎忢帪偲偟偰偺埨慡棪丄嫋梕墳椡搙偵傛傝愝寁偡傞偺偑傛偄乿偲乽嫏峘丒嫏応偺巤愝偺愝寁嶲峫恾彂 2015擭斉 [忋]乿偺p412偵婰嵹偑偁傝傑偡丅
偦偺偨傔丄梘埑椡傪峫椂偟偨応崌偼攇偺扟偲攇偺嶳偱嫋梕抣偑堎側傝傑偡丅
00367
俻仌俙.丂嶲峫暥專
- 曄埵朄偺K1,K2,K3,K4偼偳偙偵婰嵹偝傟偰偄傑偡偐
- 抧斦斀椡學悢偺寁嶼曽朄偱摴楬嫶帵曽彂偵弨嫆偟偨応崌丄姺嶼嵹壸暆B'偺嶼掕曽朄傪嫵偊偰壓偝偄
峐婎慴愝寁曋棗(暯惉4擭)偺P188乣P210偵曄埵朄丄曄宍朄(崉惈儅僩儕僋僗)丄揱払儅僩儕僋僗朄偑婰嵹偝傟偰偄傑偡丅
偙偙偱丄揱払儅僩儕僋僗朄偺K1,K2,K3,K4偼P205偵婰嵹偝傟偰偄傑偡丅
仸暰幮峐幃峔憿暔偺曄埵朄偼忋婰偺揱払儅僩儕僋僗朄丄僼儗乕儉寁嶼偼曄宍朄(崉惈儅僩儕僋僗)偲側傝傑偡丅
峐婎慴愝寁曋棗(暯惉H18擭)偵偼揱払儅僩儕僋僗朄偺K1,K2,K3,K4偺婰嵹偼偁傝傑偣傫偑丄
崉惈儅僩儕僋僗偺崁偺P361偵乽傑偨揱払儅僩儕僋僗朄偵傛傝楢棫曽掱幃偺師悢傪彮側偔偡傞偙偲傕偱偒傞丅乿偲揱払儅僩儕僋僗朄偑婰嵹偝傟偰偄傑偡丅
偙偙偱丄揱払儅僩儕僋僗朄偺K1,K2,K3,K4偼P205偵婰嵹偝傟偰偄傑偡丅
仸暰幮峐幃峔憿暔偺曄埵朄偼忋婰偺揱払儅僩儕僋僗朄丄僼儗乕儉寁嶼偼曄宍朄(崉惈儅僩儕僋僗)偲側傝傑偡丅
峐婎慴愝寁曋棗(暯惉H18擭)偵偼揱払儅僩儕僋僗朄偺K1,K2,K3,K4偺婰嵹偼偁傝傑偣傫偑丄
崉惈儅僩儕僋僗偺崁偺P361偵乽傑偨揱払儅僩儕僋僗朄偵傛傝楢棫曽掱幃偺師悢傪彮側偔偡傞偙偲傕偱偒傞丅乿偲揱払儅僩儕僋僗朄偑婰嵹偝傟偰偄傑偡丅
00623
峐婎慴峔憿暔偱偺姺嶼嵹壸暆B'偼師幃偱寁嶼偝傟傑偡丅
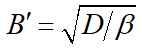
偙偙偱巊梡偝傟傞摿惈抣β偵偮偄偰
摴楬嫶帵曽彂丒摨夝愢丂嘩壓晹峔憿曇乮暯惉29擭11寧乯
P190
亀偙偙偱丄B'傪嶼掕偡傞嵺偺kH偼抧恔偺塭嬁傪娷傑側偄応崌偺抣偲偟丄愝寁忋偺抧斦柺偐傜1/β傑偱偺怺偝偺暯嬒揑側抣偲偟偰傛偄丅傑偨丄抧斦傪懡憌偲偟偰昡壙偟丄奺憌偺悈暯曽岦抧斦斀椡學悢傪嶼弌偡傞応崌傕丄奺憌偺姺嶼嵹壸暆偼忋婰偵傛傝媮傔偨B'傪梡偄傞傕偺偲偡傞亁
偙偺堦暥傛傝
丒B'傪嶼掕偡傞嵺偺KH偵梡偄傞抧斦斀椡學悢偺姺嶼學悢α偼抧恔偺塭嬁傪娷傑側偄応崌偺抣傪梡偄傞
丒B'傪嶼掕偡傞嵺偺β偼1/β傑偱偺怺偝偺暯嬒揑側抣傪梡偄傞
偲偟偰姺嶼嵹壸暆傪寁嶼偟偰偄傑偡丅
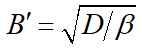
偙偙偱巊梡偝傟傞摿惈抣β偵偮偄偰
摴楬嫶帵曽彂丒摨夝愢丂嘩壓晹峔憿曇乮暯惉29擭11寧乯
P190
亀偙偙偱丄B'傪嶼掕偡傞嵺偺kH偼抧恔偺塭嬁傪娷傑側偄応崌偺抣偲偟丄愝寁忋偺抧斦柺偐傜1/β傑偱偺怺偝偺暯嬒揑側抣偲偟偰傛偄丅傑偨丄抧斦傪懡憌偲偟偰昡壙偟丄奺憌偺悈暯曽岦抧斦斀椡學悢傪嶼弌偡傞応崌傕丄奺憌偺姺嶼嵹壸暆偼忋婰偵傛傝媮傔偨B'傪梡偄傞傕偺偲偡傞亁
偙偺堦暥傛傝
丒B'傪嶼掕偡傞嵺偺KH偵梡偄傞抧斦斀椡學悢偺姺嶼學悢α偼抧恔偺塭嬁傪娷傑側偄応崌偺抣傪梡偄傞
丒B'傪嶼掕偡傞嵺偺β偼1/β傑偱偺怺偝偺暯嬒揑側抣傪梡偄傞
偲偟偰姺嶼嵹壸暆傪寁嶼偟偰偄傑偡丅
00618
俻仌俙.丂愝掕
- 揝斅旐暍偱偺僗儕僢僩偺梟愙挿偼偳偺傛偆側抣傪梡偄傑偡偐
僗儕僢僩侾忦摉偨傝偺梟愙挿偼丄幚嵺偵偼丂俀亊僗儕僢僩挿亄僗儕僢僩暆丂偵側傝傑偡偑
2009擭斉丂峘榩峔憿暔杊怘丒曗廋儅僯儏傾儖P323
亀峾斅梟愙偵偍偄偰偼墧捈曽岦偺偡傒擏梟愙偑嬋偘偵懳偟偰桳岠偱偁傝丄悈暯曽岦偡傒擏梟愙乮彫岥梟愙乯偺嬋偘掞峈岠壥偼偒傢傔偰彫偝偄
偟偨偑偭偰丄杮岺朄偺梟愙愝寁偵偍偄偰偼悈暯曽岦偡傒擏梟愙傪柍帇偟丄桳岠偺偳抐柺愊偍傛傃抐柺學悢傪媮傔偰偄傞亁偲偺婰弎傛傝
徠嵏偵娭偟偰偼丂俀亊僗儕僢僩挿丂偱峫偊傑偡丅
2009擭斉丂峘榩峔憿暔杊怘丒曗廋儅僯儏傾儖P323
亀峾斅梟愙偵偍偄偰偼墧捈曽岦偺偡傒擏梟愙偑嬋偘偵懳偟偰桳岠偱偁傝丄悈暯曽岦偡傒擏梟愙乮彫岥梟愙乯偺嬋偘掞峈岠壥偼偒傢傔偰彫偝偄
偟偨偑偭偰丄杮岺朄偺梟愙愝寁偵偍偄偰偼悈暯曽岦偡傒擏梟愙傪柍帇偟丄桳岠偺偳抐柺愊偍傛傃抐柺學悢傪媮傔偰偄傞亁偲偺婰弎傛傝
徠嵏偵娭偟偰偼丂俀亊僗儕僢僩挿丂偱峫偊傑偡丅
01933
